这篇博文以“机器学习三步走 → 模型改进 → 深度网络 → 反向传播”主线，结合 YouTube 观影量示例，帮助完全零基础读者理解深度学习核心概念与训练流程。主体内容和具体细节多来自Hylee 2021 课程第一讲1 2。

机器学习，就是找一个函数，给定输入，得到我们想要的输出。

机器学习主要有两大类任务 - 回归，分类；还有结构学习 structured learning - 画图、写文章等，让机器学会创造。

AlphaGO 也是个分类问题，不过是从 19x19 的结果中选择。

机器学习三步走

机器如何找到这个函数？课上的例子，是利用 youtube 上当前视频的过去观看信息等资料，预测明天的频道观看次数。

这个过程可以总结为三个步骤。

  • 先猜测一下，函数什么样子 - 假设函数形式

关于昨天观看次数 $x_{1}$ 的一元线性 model - $y=b+wx_{1}$，其中 $b,w$ 是未知的，$x_{1}$ 是已知的，叫做特征 feature，$w,b$ 分别为 weight 和 bias。

这个猜测，通常来自于对这个特定问题领域的知识的了解 - based on domain knowledge。

  • 定义 loss (is a function of parameters, $L(b,w)$)，输出代表着这组参数的好坏

具体的loss数值从 training data 中计算，在这个问题中，就是频道过去的观看次数，$e=|y-\hat{y}|$，其中 $y$ 就是 label - 正确的值。

$L=\frac{1}{N}\sum e_{n}$，$L$ 越大代表着参数越差，有 MAE - mean absolute error 和 MSE 等。如果 $y$ 和 $\hat{y}$ 都是概率分布的话，$L$ 可能选择使用 Cross entropy - 交叉熵。

  • 最佳化 optimization, 数学表示 $w^{opt}, b^{opt} = \arg\min_{w,b} L$

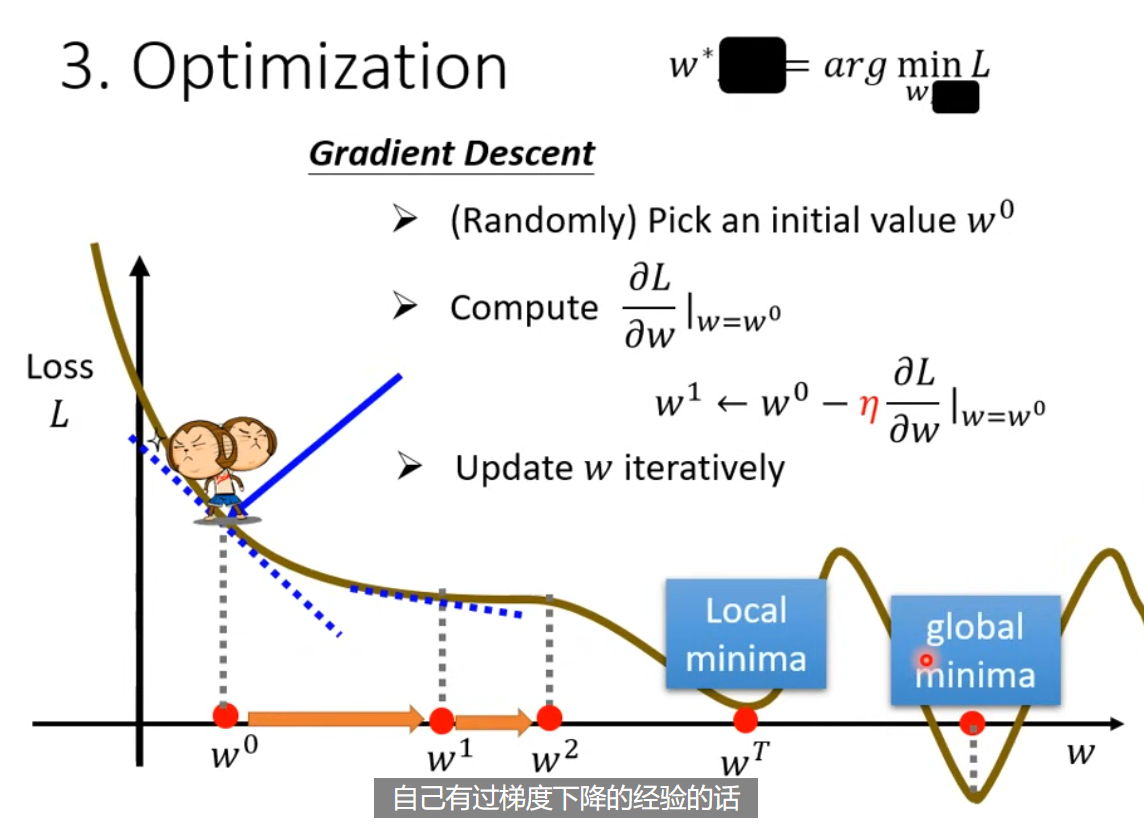
这门课中十分常用的方法就是梯度下降 - gradient descent。 以一元情况为例，随机选择初始值 $w^0$，然后计算在点的梯度/偏导数/微分 $\frac{\partial L}{\partial w} \bigg|_{w=w^0}$。

如果梯度是负数，增加参数值；梯度是正数则降低参数值；其实就是看左右，哪一边比较低，向低的方向迈一步。

这一步的大小 $\eta \times \frac{\partial L}{\partial w} \bigg|_{w=w^0}$ 取决于斜率/微分和学习率 $\eta$ (learning rate)，是个超参数 hyperparameter (自己设定的，决定参数的更新效率)。

$$ w^{1} = w^0 - \eta \frac{\partial L}{\partial w} \bigg|_{w=w^0} $$

接着反复进行移动的操作，找到 $w^T$。这个求解过程停止的时间，可能是由参数训练次数上限 - 超参数，也可能是找到微分为 0 的情况，也就是不再移动。

这就引出了，梯度下降方法的局限，就是会被损失的局部最小值困住，而找不到全局的最小值。

这个局限，在实际中是个假问题，只是个理论上的东西。真正的痛点，在之后有所讨论

Gradient descent algorithm example showing parameter update formula and iteration process

可以自然的，从一个参数推广到多参数。

微分计算的具体细节，都被大部分框架包装好了。你可以完全不知道，微分在干什么！

以上三个步骤 - 定义函数形式、定义损失函数和优化求解，合起来叫做训练。

在没看过的数据上，再进行预测和计算误差。

Simple linear regression prediction vs actual values comparison showing model prediction limitations

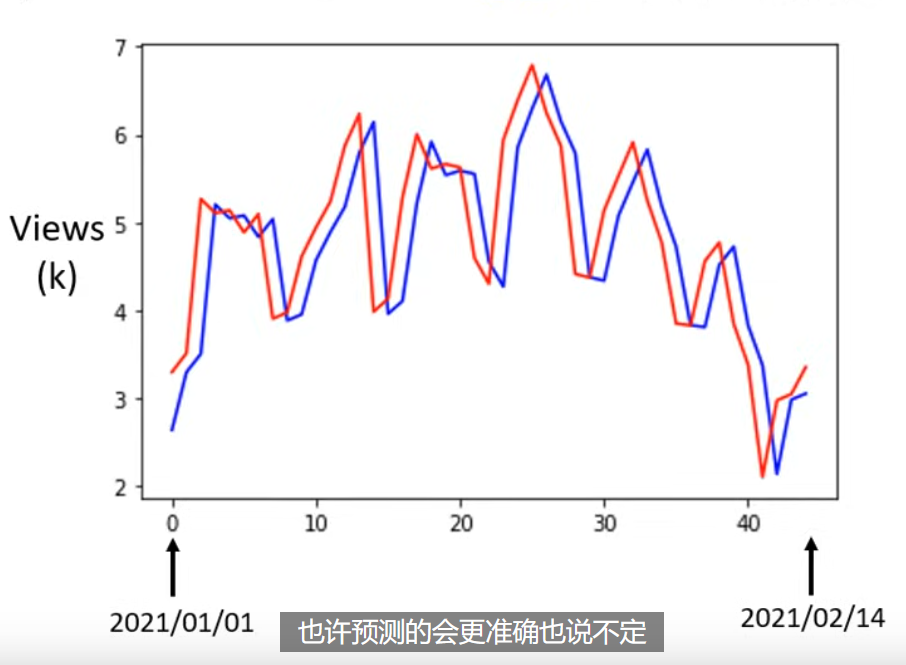
可以看到，预测值 - 蓝色线条其实只是把真实值往后移动一天而已。而真实值 - 红色线条是有周期性的，周五和周六都是比较低的。在观察到周期性之后，我们的线性 model 是很差的，他似乎只考虑了前一天的数据。

所以应该修改一下模型形式，而这个修改，应该来自我们对问题的理解。考虑新模型 $y=b+\sum^7_{j=1}w_{j}x_{j}$ ，计算后发现，训练 loss 降低了，在测试 loss 上也略有降低。如果再尝试考虑 28 天的信息，训练和测试误差都更会变好一点。

流程改进

线性模型的问题是，$x,y$ 之间的线性关系，对于现实世界来说，过于简单了。这种来自 model 的限制，叫做 model bias.

Piecewise Linear Curves - 对于线性回归的改进，把曲线分解为常数 + 一系列 sigmoid。

Piecewise linear curve example showing how to fit complex functions with multiple linear segments

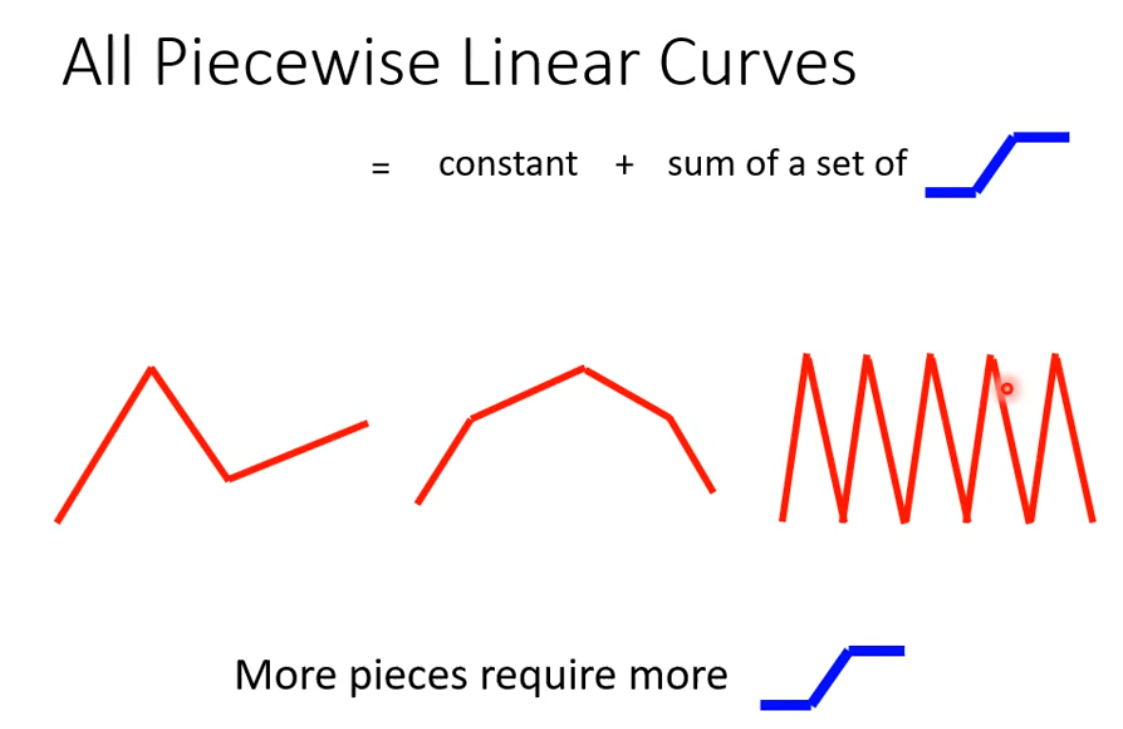
如果是曲线形状，是一样可以化为近似折线情形的。piecewise linear 可以拟合任意连续曲线。

Piecewise linear approximation of nonlinear function showing how piecewise linear can fit any continuous curve

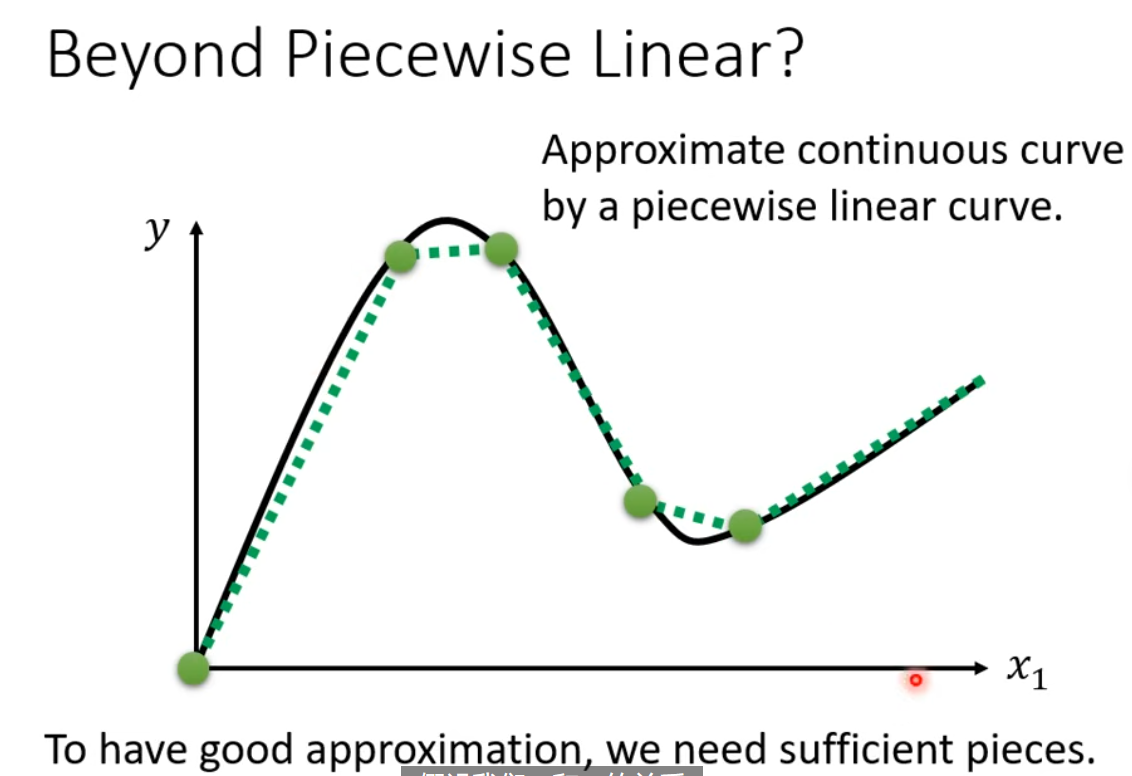
上面的蓝色折线，用 sigmoid 曲线进行逼近，$y=c \frac{1}{1+e^{-(b+wx_{1})}}=c\times sigmoid(b+wx_{1})$，蓝色的曲线，一般可以叫做 hard sigmoid。不同的 sigmoid 形状，就是由不同程度 $c,w,b$ 构成。

Sigmoid function shape changes under different parameters w, b, c

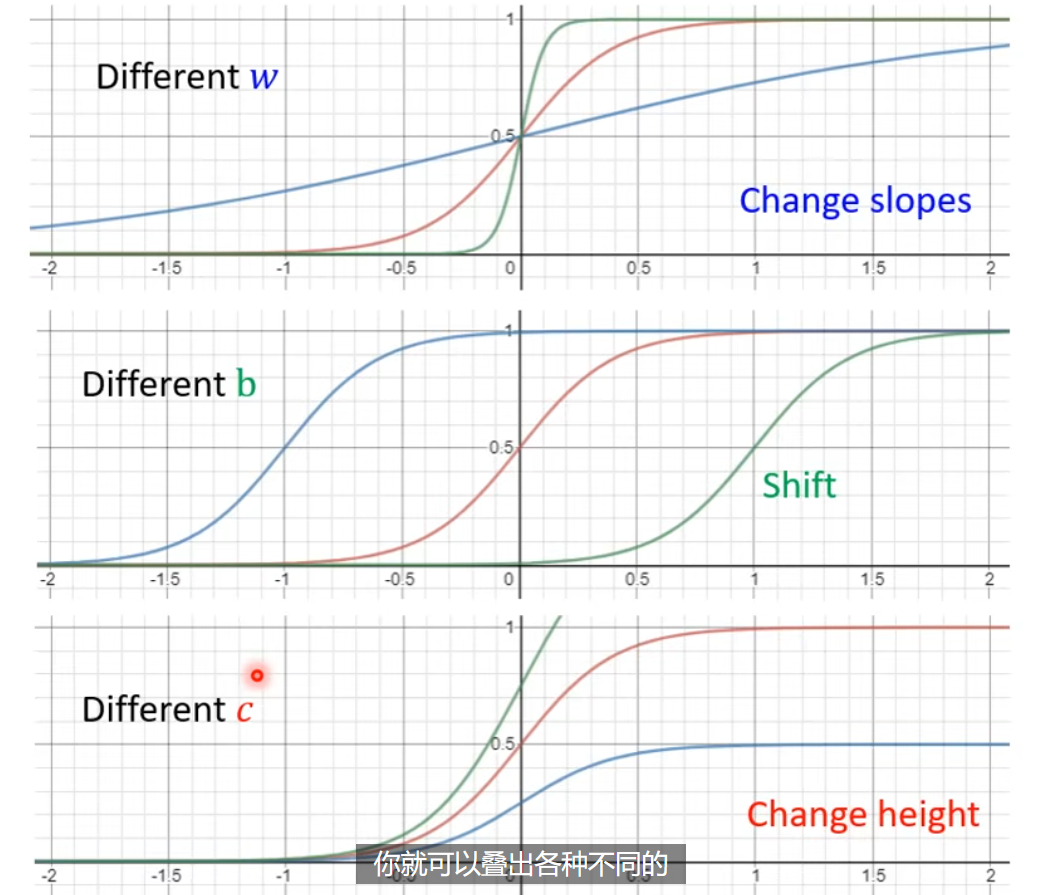
新的一元函数用可以形如 $y=b+\sum c_{i}\times sigmoid(b_{i}+w_{i}x_{1})$来近似拟合。多元函数的具体见下图：

sigmoid 的数量是可以自定义的，这是另一个超参数。sigmoid 数量越多，就越能拟合复杂的情形。

Mathematical representation of weighted sum of multiple sigmoid functions fitting complex function

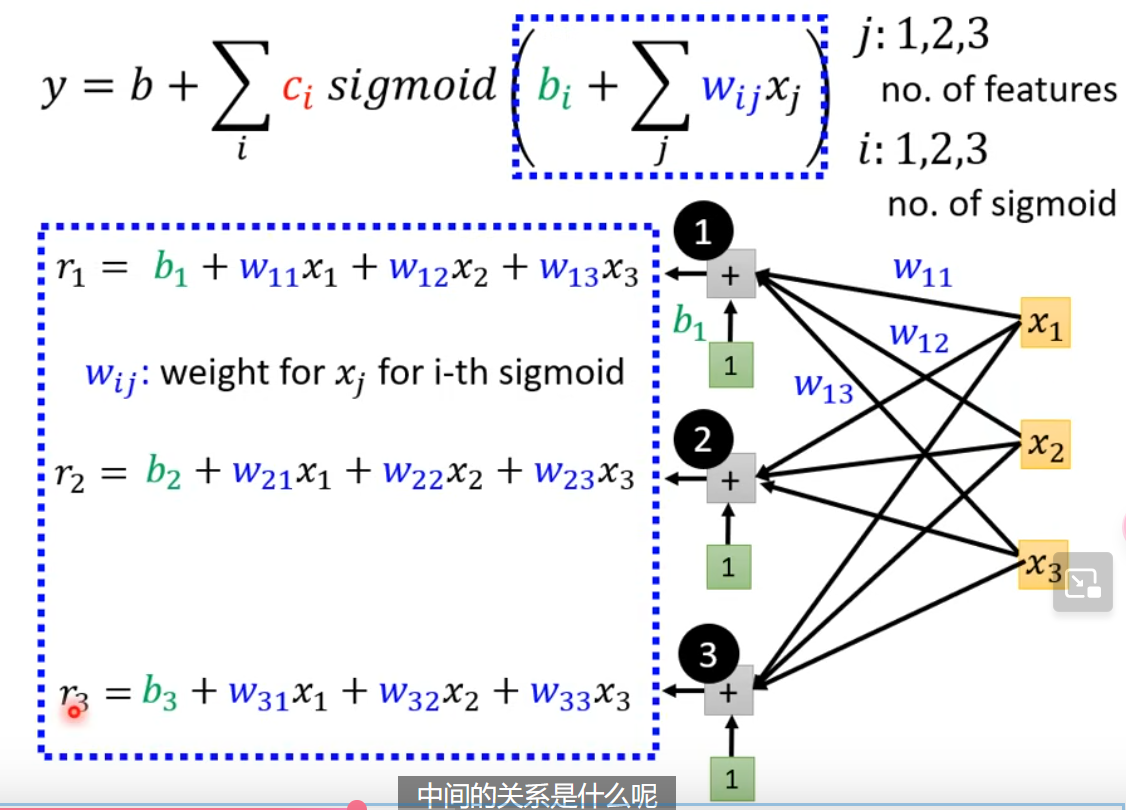
进一步利用向量乘法，$\mathbf{r}=\mathbf{b}+W\mathbf{x}$，$\mathbf{a}=\sigma(\mathbf{r})$，其中 $a_{1}=sigmoid(r_{1})$，$y=b+\mathbf{c}^T\mathbf{a}$，具体见下图

Sigmoid function weighted sum model structure using vector notation

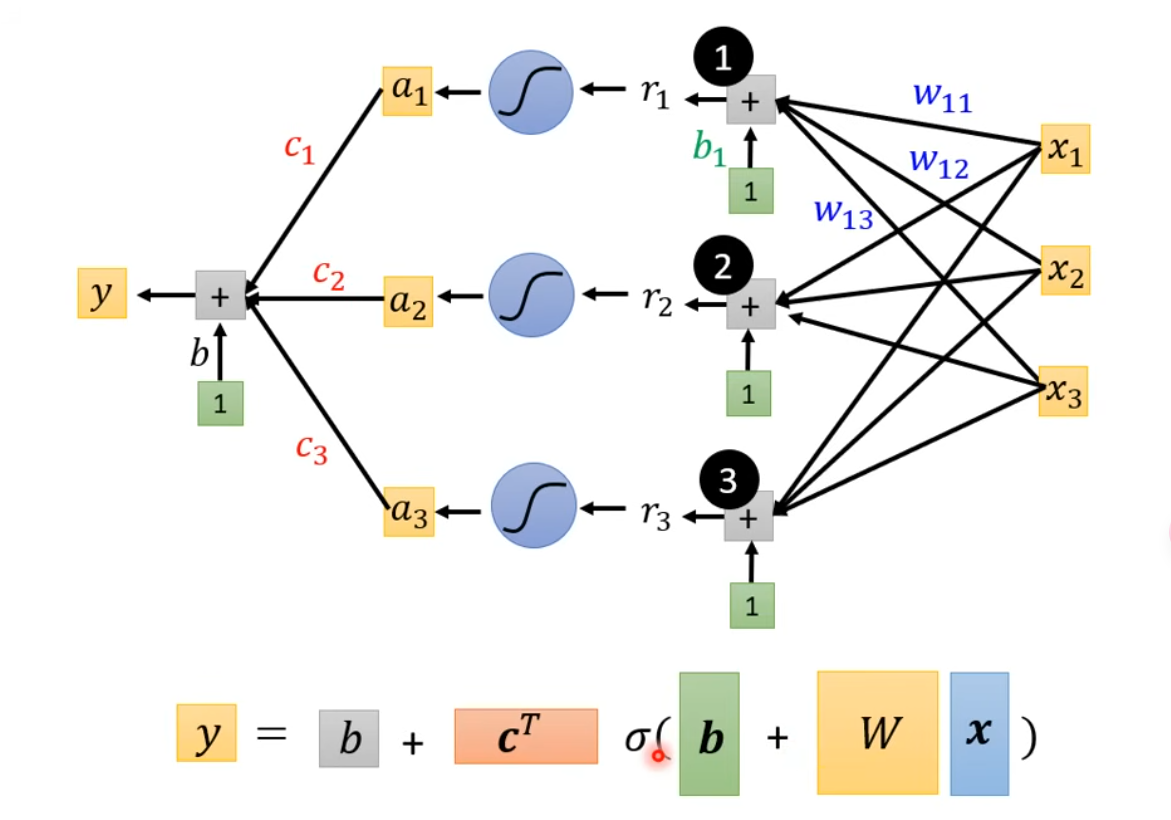
注意，此时我们就把机器学习三步走中的第一步，定义带有未知数的函数形式，变成了上图的形式。

模型还有更多的变形，比如把 sigmoid 换成 ReLU - Rectified Linear Unit - $c\times \max(0, b+wx_{1})$，两个 ReLU 就可以合成一个上面所说的 hard sigmoid。sigmoid 和 ReLU 叫做 activation function - 激活函数。

改进之后的 Loss $L(\theta)$，本质上没有什么变化。引入一个新的参数 $\theta$，其代表了所有的需要估计的参数。

改进后的 optimization 也与之前没什么区别，方法还是梯度下降找最下损失。梯度的表示方法见下图，本质上就是所有参数 $\theta$ 对 $L$ 的偏导数，构成了一个向量。

Vector gradient descent algorithm principle diagram for multi-parameter case

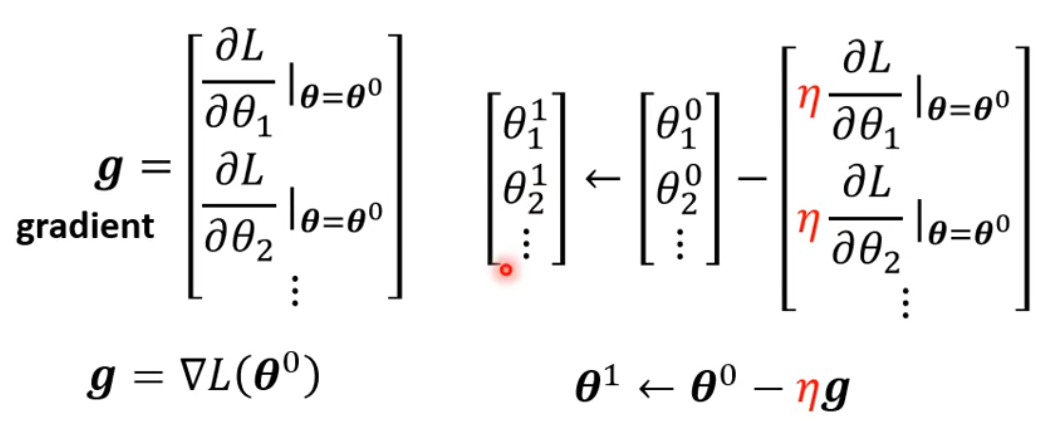
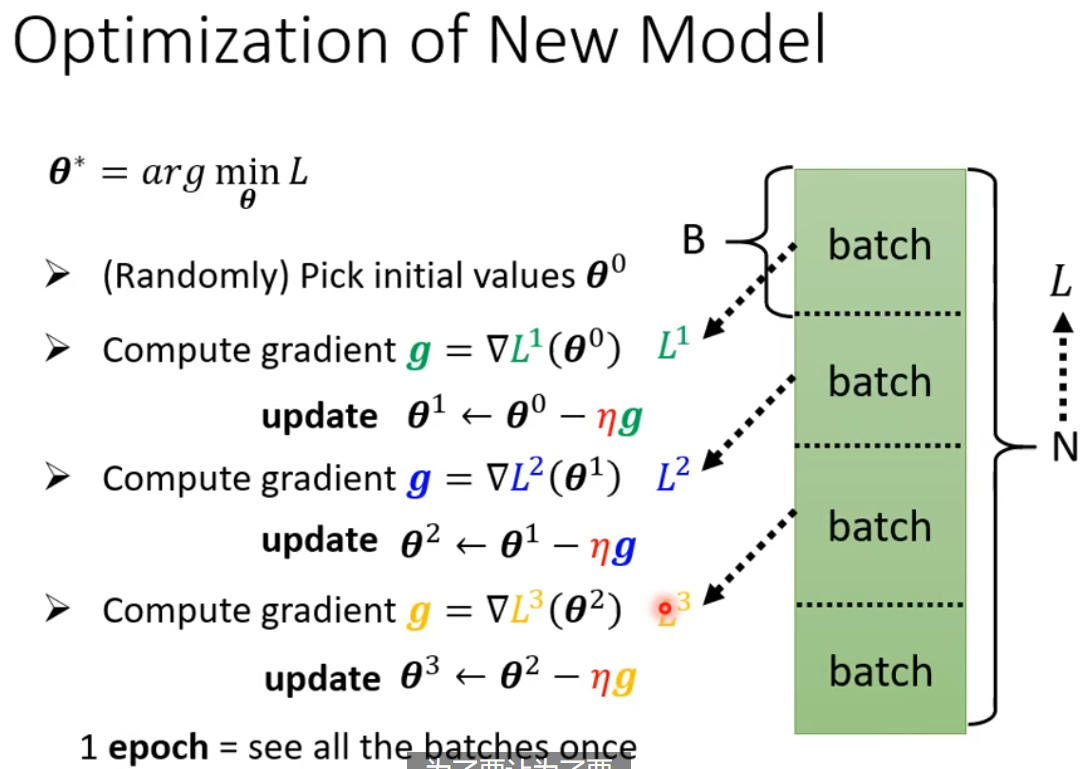
实际上，我们很难找到梯度为 0 的时候。具体代码中的更新方法，见下图。下图引出了 update 和 epoch 的区别。

一次参数更新称为一次 iteration，也常叫 step；遍历完全部样本称为一个 epoch。我们是把所有的数据分成不同的 batch（具体多少个取决于 batch size，也是个超参数），每次取一个 batch 计算 loss 和梯度，并更新 $\theta$。当见过所有的 batch 并更新参数之后，也就是一个 epoch 。

Batch gradient descent optimization process showing relationship between batch, iteration and epoch

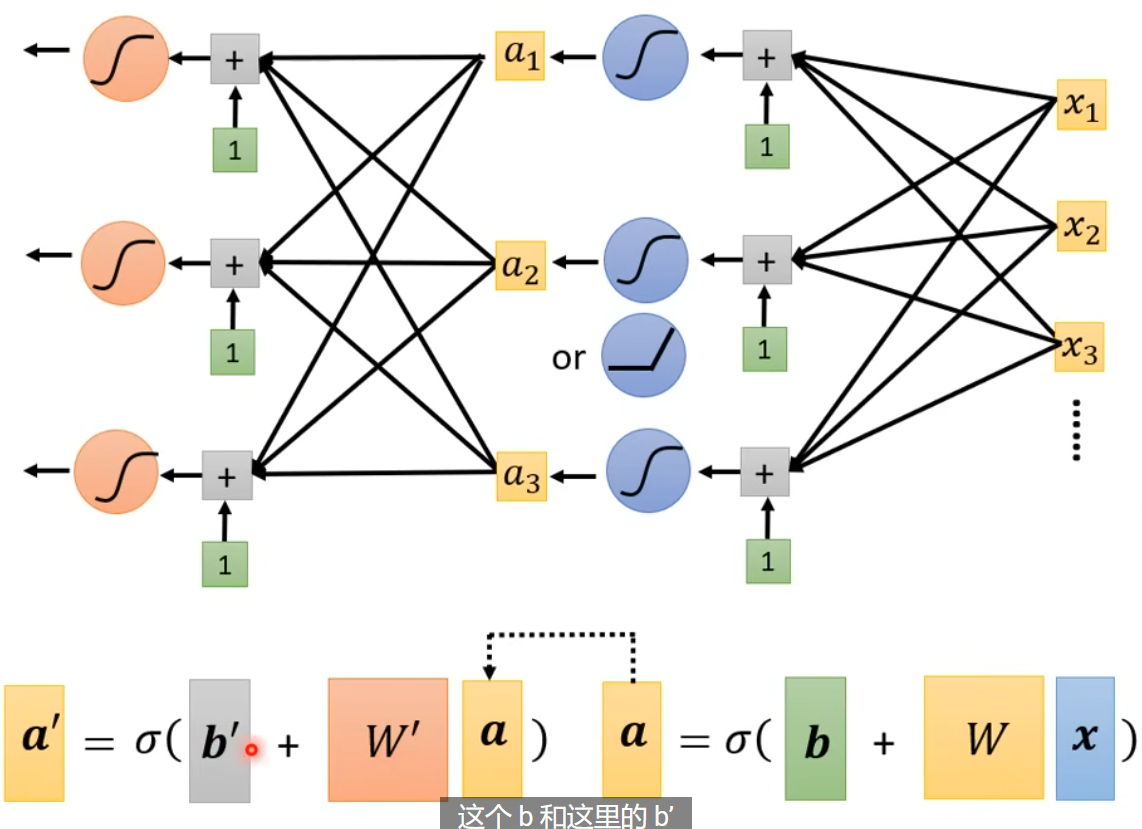
我们可以继续，套更多层的激活函数，到底嵌套多少层，这也是个超参数。

Multi-layer nested activation function structure showing hierarchical feature extraction in deep networks

深度学习

上面我们改进后的模型，就是神经网络 - 此时每个部分叫做神经元。由于神经网络名声臭掉，人们该把他们叫做隐藏层，整个重新起名字叫 - 深度学习！

Neural network structure diagram showing connections between input layer, hidden layers and output layer

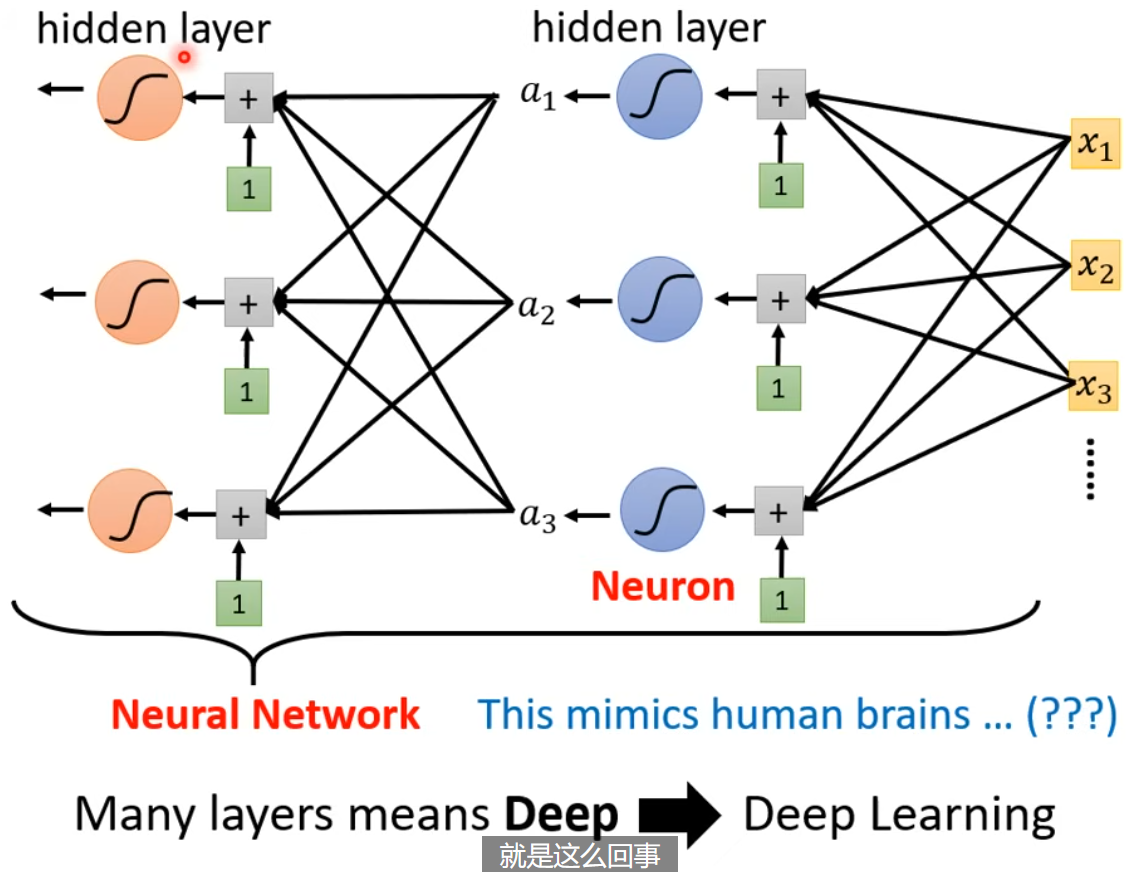
当后来，AlexNet, VGG, GoogleNet, Residual Net 把层数越做越多，这样一个问题就浮出水面。我们已经知道，足够多的 （横向排列的）sigmoid 就可以拟合任意函数，那我们为什么还要把他的层数越做越多，越做越深呢？且听后来分解。

课上利用实际的例子，发现在 4 层的时候，虽然训练 loss 有所降低，但是 test loss 反而比 3 层有所增加，这就引入了 overfitting 的概念。

Backpropagation

3

神经网络结构下，因为有海量的参数，梯度的维度是非常大的。 backpropagation 就是高效计算梯度的方法。

链式法则的复习见下图：

Chain rule mathematical principle diagram, mathematical foundation of backpropagation algorithm

如果用 $C^n$ 表示 $y^n$ 与 $\hat{y}^n$ 之间的误差，那么 $L(\theta)=\sum_{n=1}^{N} C^n(\theta)$，通过链式法则进而有 $\frac{ \partial L(\theta) }{ \partial w }=\sum_{n=1}^{N} \frac{ \partial C^n(\theta) }{ \partial w }$。尤其需要注意当 $z$ 拥有两个分量时 - Case 2，链式法则要求我们要同时考虑二者的影响。

Backpropagation algorithm overview showing forward propagation and backward propagation computation flow

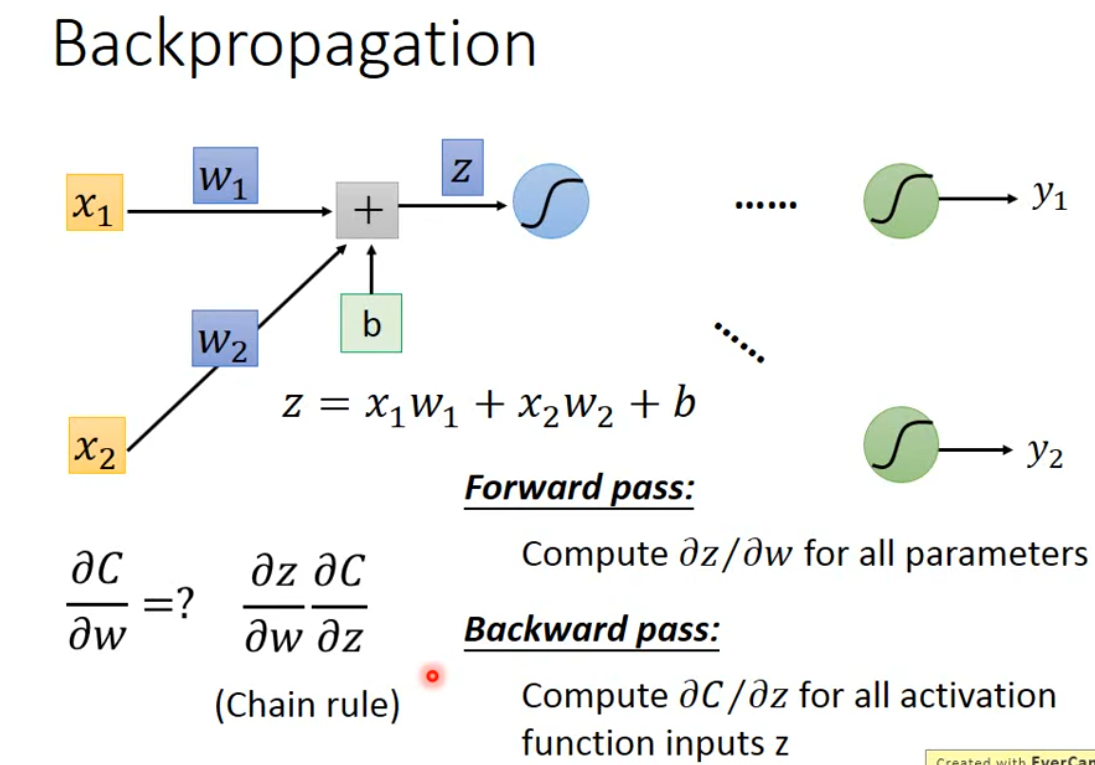
其中 $\frac{ \partial z }{ \partial w_{1} }=x_{1}, \frac{ \partial z }{ \partial w_{2} }=x_{2}$，其结果就是 $x$，计算起来是十分容易的，是我们对应 $w$ 的输入。我们结合 forward pass，具体有下图 $\frac{ \partial z }{ \partial w }=x$.

Backpropagation forward pass process showing computation steps from input to output

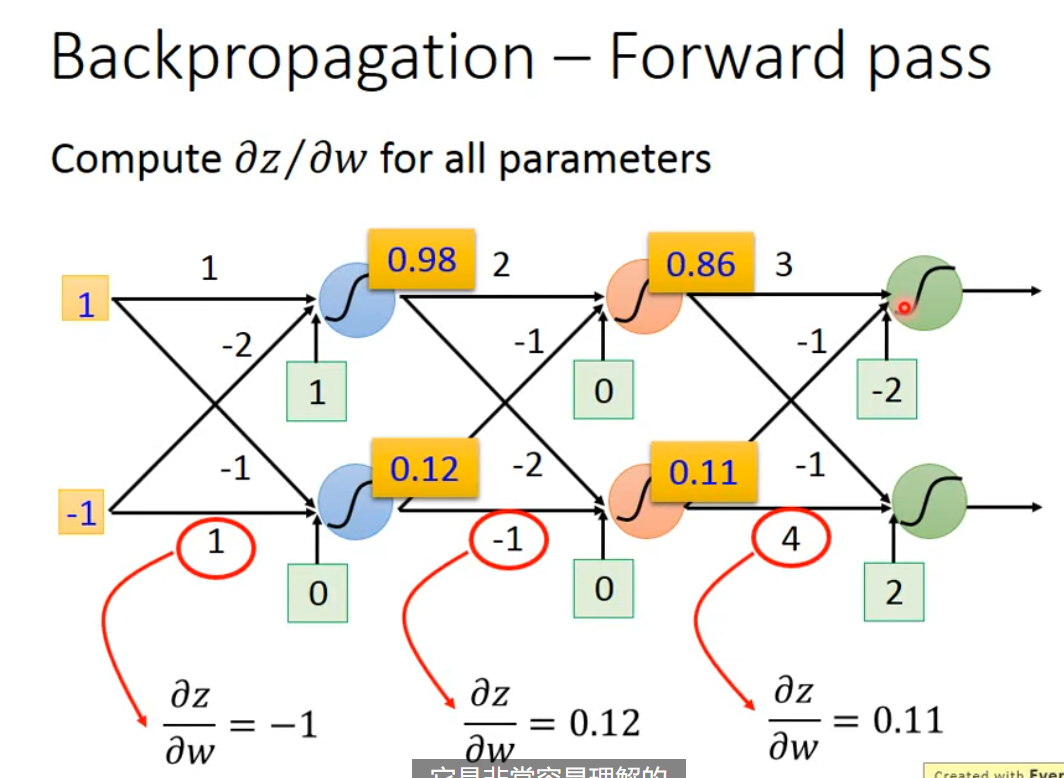
到了 backward pass $\frac{ \partial C }{ \partial z }$，问题就变得有些复杂。

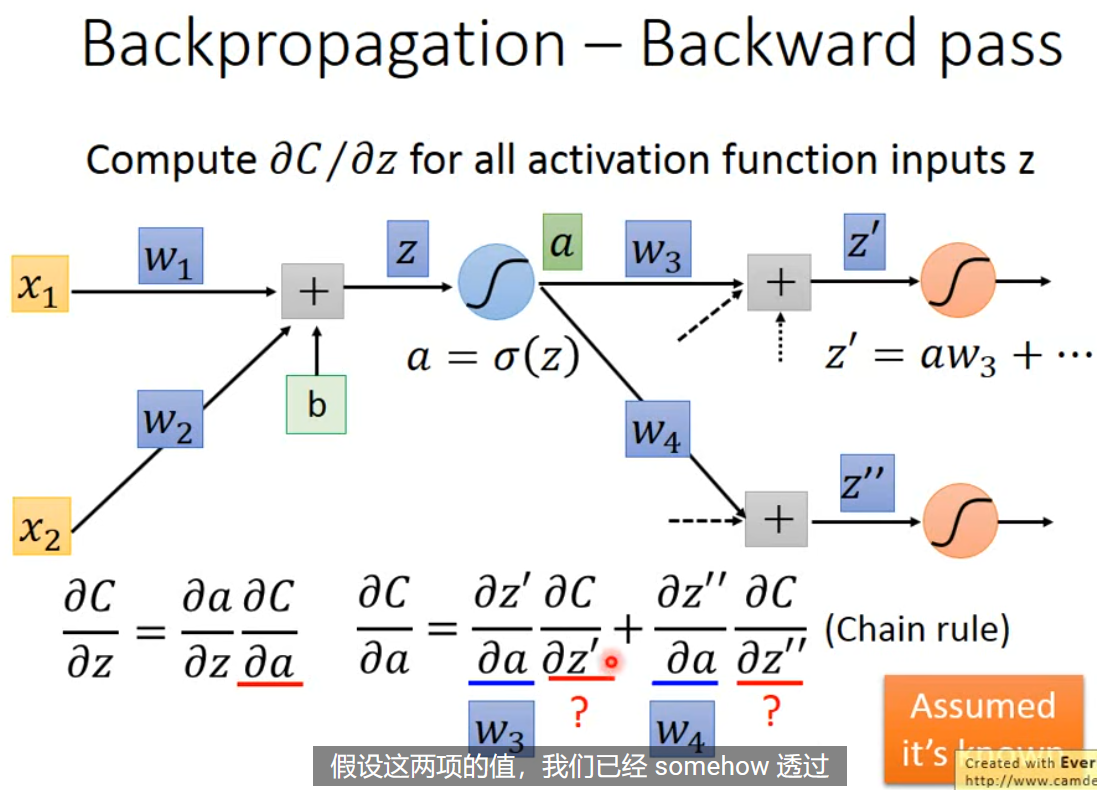
同样可以根据链式法则，进行拆分得到 $\frac{ \partial C }{ \partial z }=\frac{ \partial a }{ \partial z }\frac{ \partial C }{ \partial a }$。同时，$a=\sigma(z), \frac{ \partial a }{ \partial z }=\sigma'(z)$。问题就简化为如何计算 $\frac{ \partial C }{ \partial a }$。

通过看图，发现 z 是通过 $z',z''$ 和后续一系列对 $C$ 进行影响（这里假定只有两项，其实不一定）。不妨假设 $\frac{ \partial C }{ \partial z' }, \frac{ \partial C }{ \partial z'' }$ 已知，那么 $\frac{ \partial C }{ \partial a }=\frac{ \partial z' }{ \partial a }\frac{ \partial C }{ \partial z'} + \frac{ \partial z'' }{ \partial a }\frac{ \partial C }{ \partial z'' }=w_{3}\frac{ \partial C }{ \partial z' }+w_{4}\frac{ \partial C }{ \partial z'' }$。故 $\frac{ \partial C }{ \partial z }=\sigma'[z](w_{3}\frac{ \partial C }{ \partial z' }+w_{4}\frac{ \partial C }{ \partial z'' })$

Backpropagation backward pass process showing gradient propagation from output layer to input layer

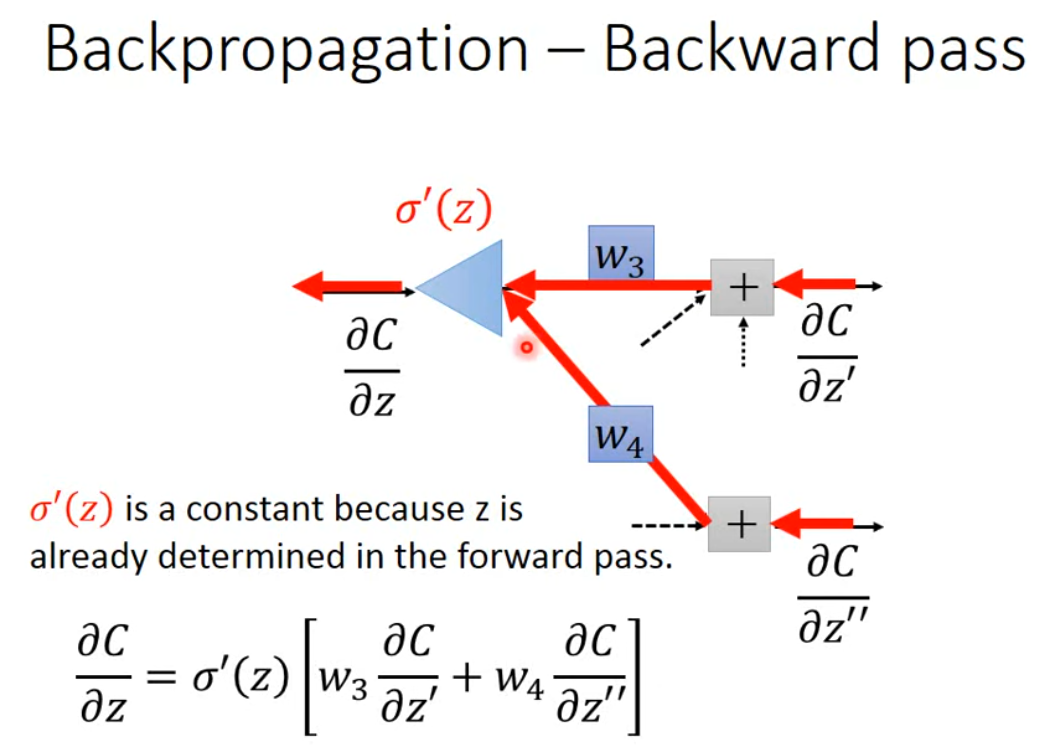
我们可以把 backward pass 看作是一个反向传播的神经网络，其中 $\frac{ \partial C }{ \partial z'}, \frac{ \partial C }{ \partial z''}$ 已知，乘上 $w$ 再通过 $\sigma'(z)$。这里注意，$\sigma'(z)$ 是个常数，因为 $z$ 已经在前向传播中，计算得到。故这个神经元其实就是个常数乘法放大因子。所有的问题，到这里就剩如何计算 $\frac{ \partial C }{ \partial z'}, \frac{ \partial C }{ \partial z''}$。

Partial derivative computation details showing specific gradient calculation methods in backpropagation

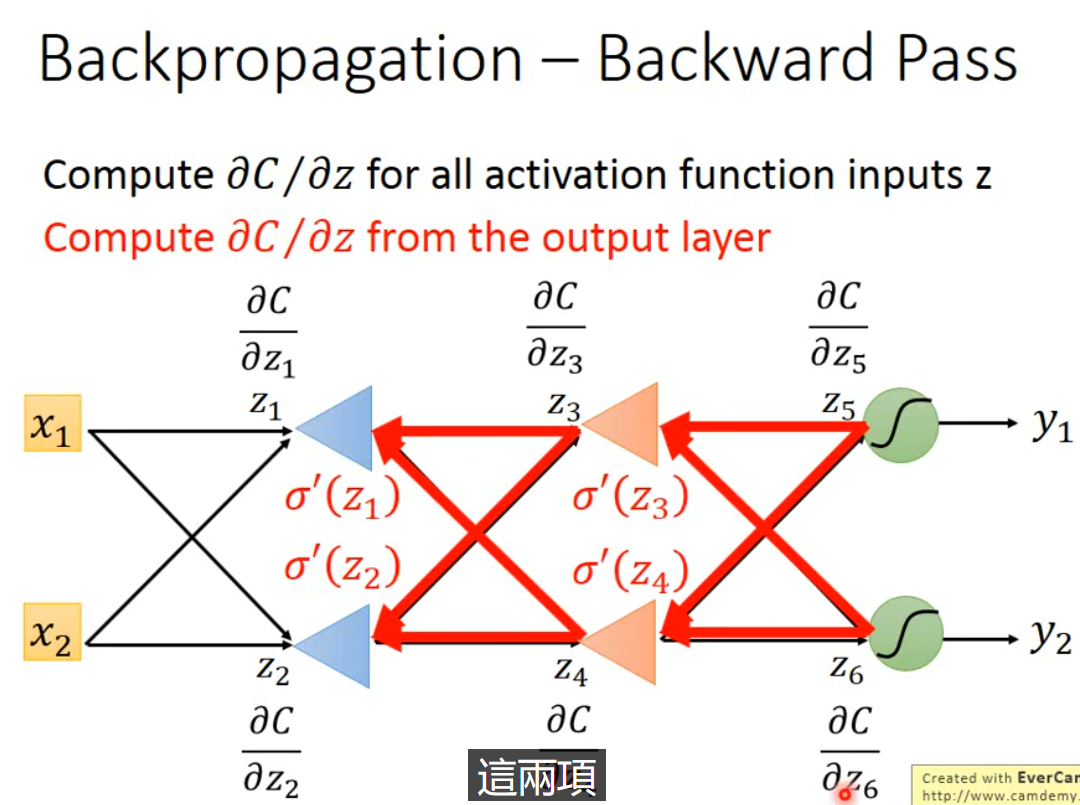
不妨假设，$z', z''$ 通过激活函数之后，已经输出了结果 $y_{1},y_{2}$。那么此时，计算 $\frac{ \partial C }{ \partial z' }=\frac{ \partial y }{ \partial z' }\frac{ \partial C }{ \partial y_{1} }$ 就变得可能，其中 $\frac{ \partial y }{ \partial z' }$ 取决于激活函数，$\frac{ \partial C }{ \partial y_{1} }$ 取决于误差形式的设定，这也是可以简单计算得到的，$\frac{ \partial C }{ \partial z'' }$ 同理。那么只要我们从后向前，真的从 $y_{1},y_{2}$ 对应的 $\frac{ \partial C }{ \partial z_{i}}$ 开始计算，再逐步往前传播，如下图。想象是从后向前算的一个新的神经网络，其中激活函数是 $\sigma'(z)$ 为常数。这样就可以计算得到我们想要的任意位置的 $\frac{ \partial C }{ \partial z }$。这就是 backward pass。

Partial derivative propagation process overview showing gradient propagation paths in the network

总结一下，当我们想计算损失函数对权重的偏微分 $\frac{ \partial C }{ \partial w }$ 用于梯度下降更新，就可以先 forward pass 计算任意位置的 $\frac{ \partial z_{i} }{ \partial w_{i} }$，然后再反向计算一遍任意位置的 $\frac{ \partial C }{ \partial z_{i} }$，这样就可以通过链式法则得到 $\frac{ \partial C }{ \partial w }=\frac{ \partial z_{i} }{ \partial w_{i} }\frac{ \partial C }{ \partial z_{i} }$，这就是 backpropagation。

Backpropagation algorithm summary diagram showing complete forward and backward propagation computation flow

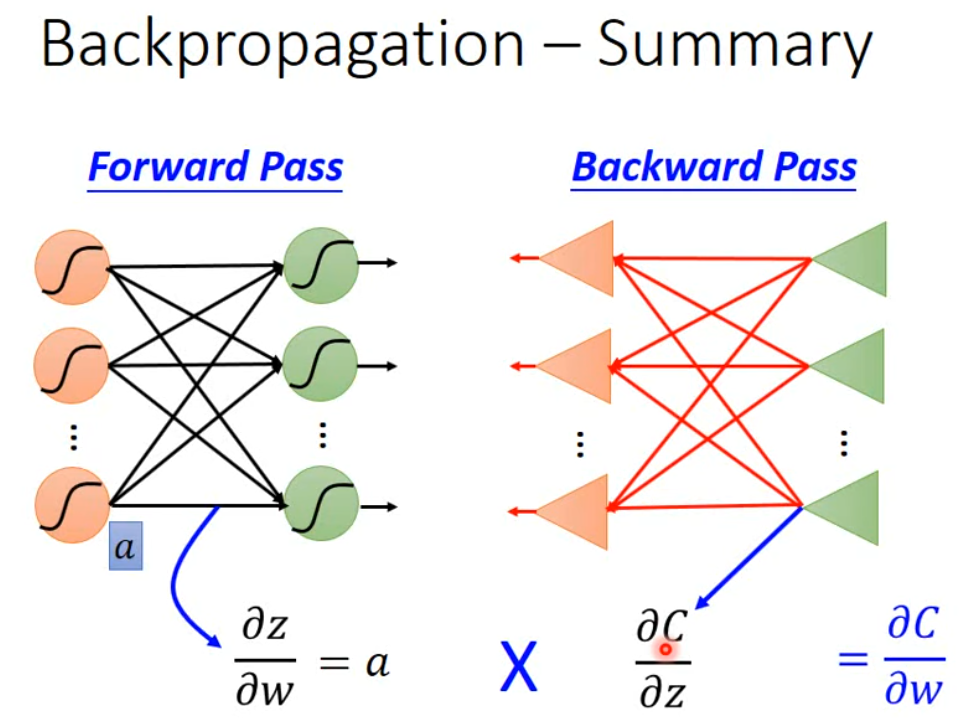
上面的演示，相比较于简单的单链条 x -> z -> a -> y -> L 略有复杂，但思路是一致的。只不过需要多考虑来自不同神经元的影响。

Sigmoid VS. ReLU

  • 梯度饱和 vs. 非饱和
    • Sigmoid 在输入很大或很小时趋近 0 或 1，此时导数 σ′(z)=σ(z)(1−σ(z))≈0，梯度几乎消失——深层网络训练困难。
    • ReLU 在 z>0 区域导数恒为 1，非饱和；z<0 区域导数为 0（稀疏激活），因此正向区域能保持梯度流动，缓解梯度消失。
  • 拟合能力（piece-wise linear 特性）
    • ReLU 本质上是 “0 或线性 “，多个 ReLU 加权可组成任意分段线性，对复杂函数拟合很灵活。
    • Sigmoid 也是非线性，但输出范围受限 $[ 0, 1]$，对某些需要 " 负激活 " 或大幅度变化的场景限制较多。
  • 计算效率
    • Sigmoid 需要 exp(·) 运算
    • ReLU 只需 max(0, z)，在硬件上极其便宜。
  • 输出分布 & 收敛速度
    • Sigmoid 输出均为正，导致后续层输入均为正，易造成 " 均值偏移 “，需要特别初始化或 BatchNorm 去缓解。
    • ReLU 有 50 % 左右概率给 0，激活更稀疏，常被认为有 " 天然正则化 " 效果，且收敛往往更快。
  • 潜在缺点
    • ReLU 的 “dead neuron” 问题：若大量权重让 z<0，则该神经元梯度永远 0，不再更新。可用 Leaky-ReLU、ELU 等改进。
    • Sigmoid 虽有梯度消失，但在输出层做 " 概率 " 解释（如二分类）仍很受欢迎。

Reference

  1. https://www.youtube.com/watch?v=Ye018rCVvOo&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J ↩︎

  2. https://www.youtube.com/watch?v=bHcJCp2Fyxs&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=2 ↩︎

  3. https://www.youtube.com/watch?v=ibJpTrp5mcE ↩︎