这是 MIT 6.006 算法导论课程的第二讲笔记,主要介绍了数据结构和接口的区别,以及静态数组、链表和动态数组在实现队列的时间复杂度分析。
Interface(API) vs. Data structure
Interface
是一种规范 (specification),关于储存什么数据、可以进行哪些操作,是 " 问题 "
这节关注两种主要的 API,set & sequence
data structure
是一种表示 (representation),关于如何储存数据、应该使用哪些算法去支持相应操作,是 " 答案 "
两种主要的 DS,arrays & pointered based
Static sequence interface
build(x) - make new; len(); iter_seq() - 注意保持顺序;get_at(i); set_at(i); get_first/last; set_first/last
解决/DS:很自然的想到,静态数组 - static array
array - 是一块连续的内存,那么访问
array[i]时,就等价于访问memory[address(arrray)+i],这也就意味着可以以常数时间 get_at(i) 和 set_at(i)
O(1) - get_at(i); set_at(i); len()
O(n) - build; iter_seq;
memory allocation model: 创建大小为 n 数组的时间复杂度为 $\Theta(n)$;同时空间复杂度为 O(n)
Synamic sequence interface
增加两个动态操作 insert_at(i, x) - 这意味着第 i 个位置之后的元素都需要进行偏移; delete_at(i); insert/delete_first/last()
可能在某些数据结构下,在首尾插入和删除可能是常数时间 - 虽然可能在 get_at(i) 无法实现常数
Linked lists - DS

注意到,他们在实际内存中的顺序可能是任意的。
指针只是储存了下一个 item 的地址。
Dyanamic sequence operation
static array
insert/delete_at() - $\Theta(n)$ 时间: 偏移操作/shift;即使是开头和结尾的元素,也需要 shift,因为 static array 在内存分配的时候,只索取了固定大小 $n$ 的空间,其左右空间可能都已经占满了,当需要 n+1 时,不得不进行 shift 以找到一块 n+1 的空位置,然后复制,这就是 allocation/copying;
linked list
与 静态数组几乎相反
insert/delete_first 是 $O(1)$ 时间 - 直接改变首项的指针;
get/set_at(i) 是 $\Theta(i)$ 时间,最坏就是 $\Theta(n)$,因为要一个一个指针从头找过去
如果想 get/insert_last 常数时间,只需要增加一个指向尾部的指针
Dyanamic Arrays - Python’s lists
放松数组大小正好等于 $n$ 的限制,而是设置为大概为 $n$;强制大小为 $\Theta(n)\geq n$ - 常数乘
仍然保持 A[i]=x_i,空白项在后面;insert_last 是常数的,只需要 A[len]=x, len+=1
同时 会储存数组的大小,注意这里 size(DS) - 分配的内存 和 len(interface) - 非空 item 的区别;当 size = len 就需要重新分配空间
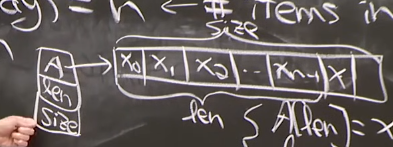
重新分配空间在动态数组中 - 通常是 $2*size$,是偶尔的行为;在静态数组中则是每次添加都需要重新分配;
下图解释了为什么动态数组的分配是线性时间 $\Theta(n)$ 的(涉及到几何级数求和) - $O(1)$ amortized; 进而我们发现了 Amortization 的概念 - 把高成本分摊给其他低成本的操作,平均而言还是不错的 almost good
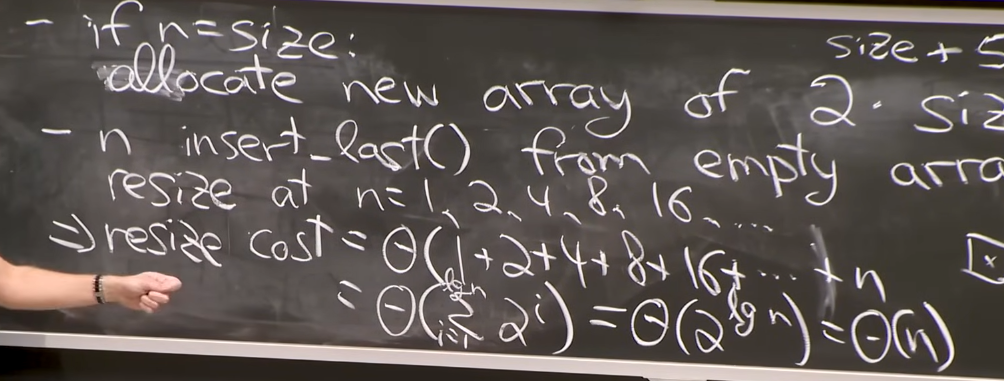
总结对比

copy_forward VS. copy_backward
之所以有 forward 和 backward 的区分,在 python 中是因为类似 A=self.A 是引用,而不是直接的 copy。
引用,指的是二者指向同一块内存地址,而 copy 是需要申请一块新的并把原来的复制过去。
这种引用的特性,也就产生了可能 overlap 的问题。例如,把 [1,2,3,4,5] 从 index=1 开始移动一个位置 - shift right by one position,如果使用 copy_forward 则是从 index =1 开始,A[2]=self.A[1]=2,按照 forward 的算法,接下来是 A[3]=self.A[2] 但此时的 self.A[2] 已经被前一步的时候更改过,不是 3 而是 2,在以此类推进行 A[4]=self.A[3]=2,最后的结果为 [1,2,2,2,2] 而不是我们想要的 [1,2,2,3,4]。我们采用 backward,首先从 A[4]=self.A[3]=4 开始,第二步是 A[3]=self.A[2]=3,注意到主要的区别就在这里,第二步我们需要的 self.A[2] 并没有被第一步更改,故继续按照 backward 算法进行,A[2]=self.A[1]=2,最后的结果为 [1,2,2,3,4] 正如我们想要!
Reference
https://ocw.mit.edu/courses/6-006-introduction-to-algorithms-spring-2020/
https://ocw.mit.edu/courses/6-006-introduction-to-algorithms-spring-2020/resources/mit6_006s20_lec2/